
Special thanks to Vlad Zamfir, Chris Barnett and Dominic Williams for ideas and inspiration
In a recent blog post I outlined some partial solutions to scalability, all of which fit into the umbrella of Ethereum 1.0 as it stands. Specialized micropayment protocols such as channels and probabilistic payment systems could be used to make small payments, using the blockchain either only for eventual settlement, or only probabilistically. For some computation-heavy applications, computation can be done by one party by default, but in a way that can be “pulled down” to be audited by the entire chain if someone suspects malfeasance. However, these approaches are all necessarily application-specific, and far from ideal. In this post, I describe a more comprehensive approach, which, while coming at the cost of some “fragility” concerns, does provide a solution which is much closer to being universal.
Understanding the Objective
First of all, before we get into the details, we need to get a much deeper understanding of what we actually want. What do we mean by scalability, particularly in an Ethereum context? In the context of a Bitcoin-like currency, the answer is relatively simple; we want to be able to:
- Process tens of thousands of transactions per second
- Provide a transaction fee of less than $0.001
- Do it all while maintaining security against at least 25% attacks and without highly centralized full nodes
The first goal alone is easy; we just remove the block size limit and let the blockchain naturally grow until it becomes that large, and the economy takes care of itself to force smaller full nodes to continue to drop out until the only three full nodes left are run by GHash.io, Coinbase and Circle. At that point, some balance will emerge between fees and size, as excessize size leads to more centralization which leads to more fees due to monopoly pricing. In order to achieve the second, we can simply have many altcoins. To achieve all three combined, however, we need to break through a fundamental barrier posed by Bitcoin and all other existing cryptocurrencies, and create a system that works without the existence of any “full nodes” that need to process every transaction.
In an Ethereum context, the definition of scalability gets a little more complicated. Ethereum is, fundamentally, a platform for “dapps”, and within that mandate there are two kinds of scalability that are relevant:
- Allow lots and lots of people to build dapps, and keep the transaction fees low
- Allow each individual dapp to be scalable according to a definition similar to that for Bitcoin
The first is inherently easier than the second. The only property that the “build lots and lots of alt-Etherea” approach does not have is that each individual alt-Ethereum has relatively weak security; at a size of 1000 alt-Etherea, each one would be vulnerable to a 0.1% attack from the point of view of the whole system (that 0.1% is for externally-sourced attacks; internally-sourced attacks, the equivalent of GHash.io and Discus Fish colluding, would take only 0.05%). If we can find some way for all alt-Etherea to share consensus strength, eg. some version of merged mining that makes each chain receive the strength of the entire pack without requiring the existence of miners that know about all chains simultaneously, then we would be done.
The second is more problematic, because it leads to the same fragility property that arises from scaling Bitcoin the currency: if every node sees only a small part of the state, and arbitrary amounts of BTC can legitimately appear in any part of the state originating from any part of the state (such fungibility is part of the definition of a currency), then one can intuitively see how forgery attacks might spread through the blockchain undetected until it is too late to revert everything without substantial system-wide disruption via a global revert.
Reinventing the Wheel
We’ll start off by describing a relatively simple model that does provide both kinds of scalability, but provides the second only in a very weak and costly way; essentially, we have just enough intra-dapp scalability to ensure asset fungibility, but not much more. The model works as follows:
Suppose that the global Ethereum state (ie. all accounts, contracts and balances) is split up into N parts (“substates”) (think 10 <= N <= 200). Anyone can set up an account on any substate, and one can send a transaction to any substate by adding a substate number flag to it, but ordinary transactions can only send a message to an account in the same substate as the sender. However, to ensure security and cross-transmissibility, we add some more features. First, there is also a special “hub substate”, which contains only a list of messages, of the form [dest_substate, address, value, data]. Second, there is an opcode CROSS_SEND, which takes those four parameters as arguments, and sends such a one-way message enroute to the destination substate.
Miners mine blocks on some substate s[j], and each block on s[j] is simultaneously a block in the hub chain. Each block on s[j] has as dependencies the previous block on s[j] and the previous block on the hub chain. For example, with N = 2, the chain would look something like this:
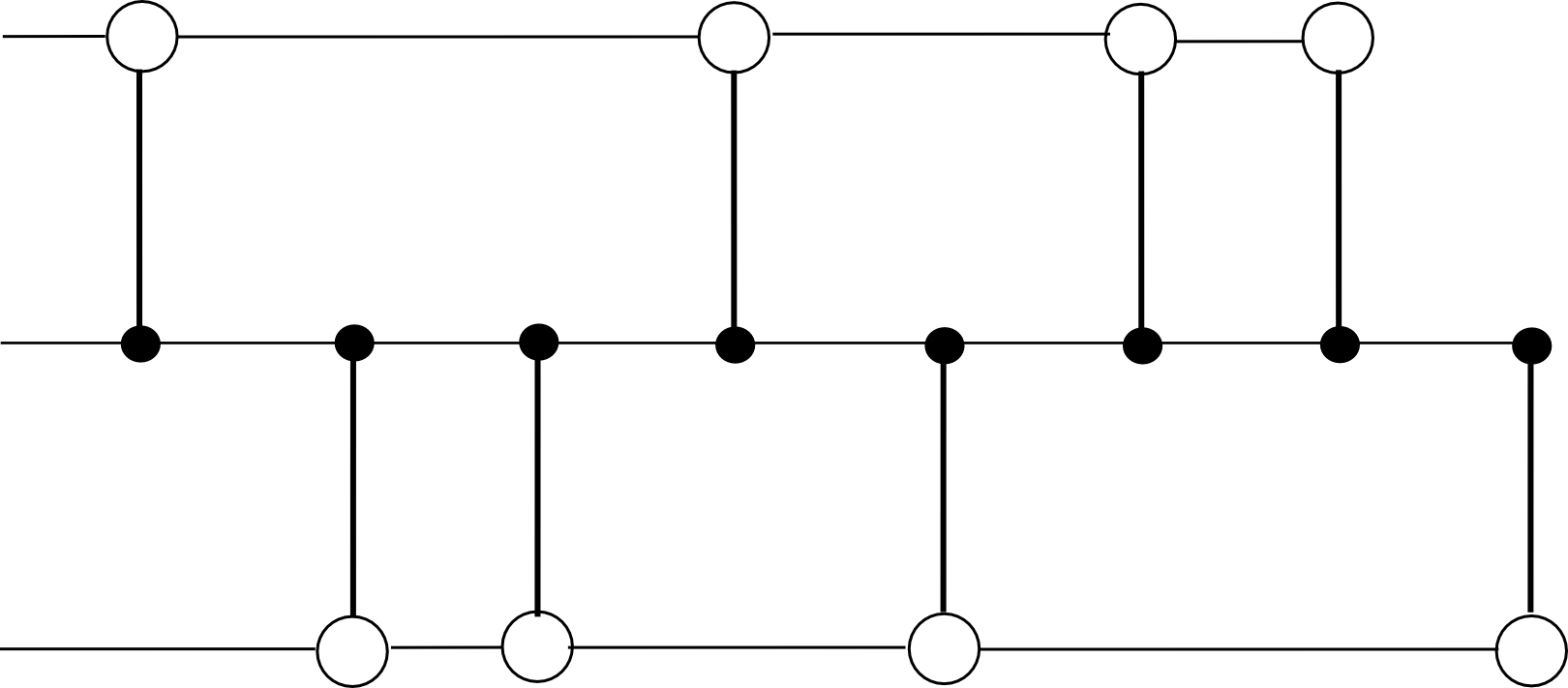
The block-level state transition function, if mining on substate s[j], does three things:
- Processes state transitions inside of s[j]
- If any of those state transitions creates a CROSS_SEND, adds that message to the hub chain
- If any messages are on the hub chain with dest_substate = j, removes the messages from the hub chain, sends the messages to their destination addresses on s[j], and processes all resulting state transitions
From a scalability perspective, this gives us a substantial improvement. All miners only need to be aware of two out of the total N + 1 substates: their own substate, and the hub substate. Dapps that are small and self-contained will exist on one substate, and dapps that want to exist across multiple substates will need to send messages through the hub. For example a cross-substate currency dapp would maintain a contract on all substates, and each contract would have an API that allows a user to destroy currency units inside of one substate in exchange for the contract sending a message that would lead to the user being credited the same amount on another substate.
Messages going through the hub do need to be seen by every node, so these will be expensive; however, in the case of ether or sub-currencies we only need the transfer mechanism to be used occasionally for settlement, doing off-chain inter-substate exchange for most transfers.
Attacks, Challenges and Responses
Now, let us take this simple scheme and analyze its security properties (for illustrative purposes, we’ll use N = 100). First of all, the scheme is secure against double-spend attacks up to 50% of the total hashpower; the reason is that every sub-chain is essentially merge-mined with every other sub-chain, with each block reinforcing the security of all sub-chains simultaneously.
However, there are more dangerous classes of attacks as well. Suppose that a hostile attacker with 4% hashpower jumps onto one of the substates, thereby now comprising 80% of the mining power on it. Now, that attacker mines blocks that are invalid – for example, the attacker includes a state transition that creates messages sending 1000000 ETH to every other substate out of nowhere. Other miners on the same substate will recognize the hostile miner’s blocks as invalid, but this is irrelevant; they are only a very small part of the total network, and only 20% of that substate. The miners on other substates don’t know that the attacker’s blocks are invalid, because they have no knowledge of the state of the “captured substate”, so at first glance it seems as though they might blindly accept them.
Fortunately, here the solution here is more complex, but still well within the reach of what we currently know works: as soon as one of the few legitimate miners on the captured substate processes the invalid block, they will see that it’s invalid, and therefore that it’s invalid in some particular place. From there, they will be able to create a light-client Merkle tree proof showing that that particular part of the state transition was invalid. To explain how this works in some detail, a light client proof consists of three things:
- The intermediate state root that the state transition started from
- The intermediate state root that the state transition ended at
- The subset of Patricia tree nodes that are accessed or modified in the process of executing the state transition
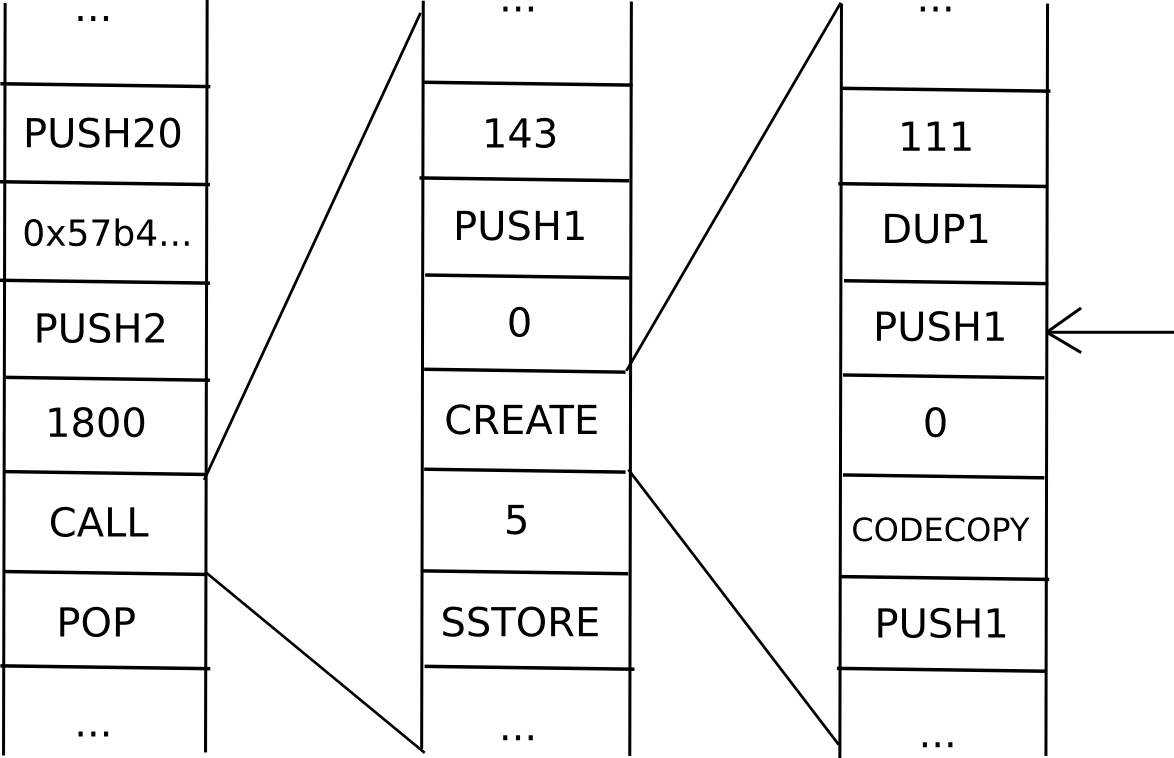
The first two “intermediate state roots” are the roots of the Ethereum Patricia state tree before and after executing the transaction; the Ethereum protocol requires both of these to be in every block. The Patricia state tree nodes provided are needed in order to the verifier to follow along the computation themselves, and see that the same result is arrived at the end. For example, if a transaction ends up modifying the state of three accounts, the set of tree nodes that will need to be provided might look something like this:
Technically, the proof should include the set of Patricia tree nodes that are needed to access the intermediate state roots and the transaction as well, but that’s a relatively minor detail. Altogether, one can think of the proof as consisting of the minimal amount of information from the blockchain needed to process that particular transaction, plus some extra nodes to prove that those bits of the blockchain are actually in the current state. Once the whistleblower creates this proof, they will then be broadcasted to the network, and all other miners will see the proof and discard the defective block.
The hardest class of attack of all, however, is what is called a “data unavailability attack”. Here, imagine that the miner sends out only the block header to the network, as well as the list of messages to add to the hub, but does not provide any of the transactions, intermediate state roots or anything else. Now, we have a problem. Theoretically, it is entirely possible that the block is completely legitimate; the block could have been properly constructed by gathering some transactions from a few millionaires who happened to be really generous. In reality, of course, this is not the case, and the block is a fraud, but the fact that the data is not available at all makes it impossible to construct an affirmative proof of the fraud. The 20% honest miners on the captured substate may yell and squeal, but they have no proof at all, and any protocol that did heed their words would necessarily fall to a 0.2% denial-of-service attack where the miner captures 20% of a substate and pretends that the other 80% of miners on that substate are conspiring against him.
To solve this problem, we need something called a challenge-response protocol. Essentially, the mechanism works as follows:
- Honest miners on the captured substate see the header-only block.
- An honest miner sends out a “challenge” in the form of an index (ie. a number).
- If the producer of the block can submit a “response” to the challenge, consisting of a light-client proof that the transaction execution at the given index was executed legitimately (or a proof that the given index is greater than the number of transactions in the block), then the challenge is deemed answered.
- If a challenge goes unanswered for a few seconds, miners on other substates consider the block suspicious and refuse to mine on it (the game-theoretic justification for why is the same as always: because they suspect that others will use the same strategy, and there is no point mining on a substate that will soon be orphaned)
Note that the mechanism requires a few added complexities on order to work. If a block is published alongside all of its transactions except for a few, then the challenge-response protocol could quickly go through them all and discard the block. However, if a block was published truly headers-only, then if the block contained hundreds of transactions, hundreds of challenges would be required. One heuristic approach to solving the problem is that miners receiving a block should privately pick some random nonces, send out a few challenges for those nonces to some known miners on the potentially captured substate, and if responses to all challenges do not come back immediately treat the block as suspect. Note that the miner does NOT broadcast the challenge publicly – that would give an opportunity for an attacker to quickly fill in the missing data.
The second problem is that the protocol is vulnerable to a denial-of-service attack consisting of attackers publishing very very many challenges to legitimate blocks. To solve this, making a challenge should have some cost – however, if this cost is too high then the act of making a challenge will require a very high “altruism delta”, perhaps so high that an attack will eventually come and no one will challenge it. Although some may be inclined to solve this with a market-based approach that places responsibility for making the challenge on whatever parties end up robbed by the invalid state transition, it is worth noting that it’s possible to come up with a state transition that generates new funds out of nowhere, stealing from everyone very slightly via inflation, and also compensates wealthy coin holders, creating a theft where there is no concentrated incentive to challenge it.
For a currency, one “easy solution” is capping the value of a transaction, making the entire problem have only very limited consequence. For a Turing-complete protocol the solution is more complex; the best approaches likely involve both making challenges expensive and adding a mining reward to them. There will be a specialized group of “challenge miners”, and the theory is that they will be indifferent as to which challenges to make, so even the tiniest altruism delta, enforced by software defaults, will drive them to make correct challenges. One may even try to measure how long challenges take to get responded, and more highly reward the ones that take longer.
The Twelve-Dimensional Hypercube
Note: this is NOT the same as the erasure-coding Borg cube. For more info on that, see here: https://blog.ethereum.org/2014/08/16/secret-sharing-erasure-coding-guide-aspiring-dropbox-decentralizer/
We can see two flaws in the above scheme. First, the justification that the challenge-response protocol will work is rather iffy at best, and has poor degenerate-case behavior: a substate takeover attack combined with a denial of service attack preventing challenges could potentially force an invalid block into a chain, requiring an eventual day-long revert of the entire chain when (if?) the smoke clears. There is also a fragility component here: an invalid block in any substate will invalidate all subsequent blocks in all substates. Second, cross-substate messages must still be seen by all nodes. We start off by solving the second problem, then proceed to show a possible defense to make the first problem slightly less bad, and then finally get around to solving it completely, and at the same time getting rid of proof of work.
The second flaw, the expensiveness of cross-substate messages, we solve by converting the blockchain model from this:
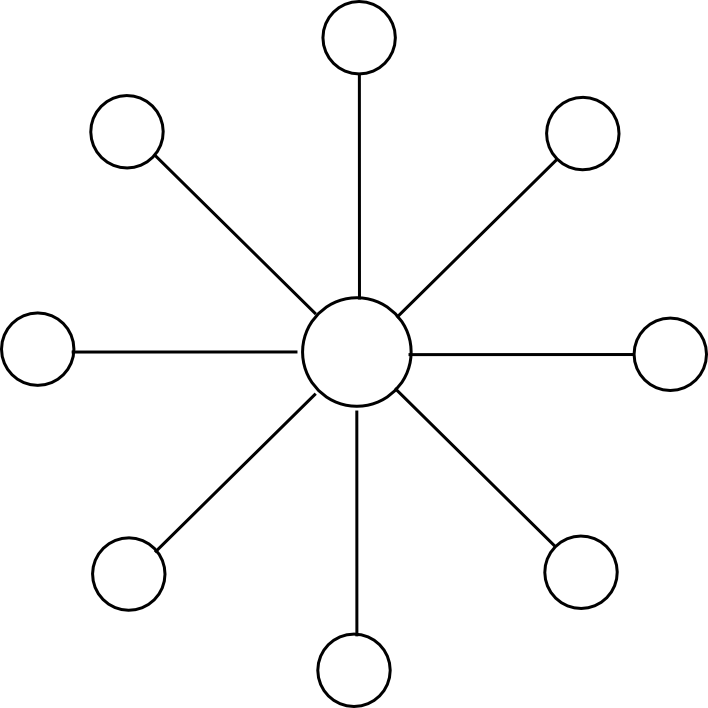
To this:

Except the cube should have twelve dimensions instead of three. Now, the protocol looks as follows:
- There exist 2N substates, each of which is identified by a binary string of length N (eg. 0010111111101). We define the Hamming distance H(S1, S2) as the number of digits that are different between the IDs of substates S1 and S2 (eg. HD(00110, 00111) = 1, HD(00110, 10010) = 2, etc).
- The state of each substate stores the ordinary state tree as before, but also an outbox.
- There exists an opcode, CROSS_SEND, which takes 4 arguments [dest_substate, to_address, value, data], and registers a message with those arguments in the outbox of S_from where S_from is the substate from which the opcode was called
- All miners must “mine an edge”; that is, valid blocks are blocks which modify two adjacent substates S_a and S_b, and can include transactions for either substate. The block-level state transition function is as follows:
- Process all transactions in order, applying the state transitions to S_a or S_b as needed.
- Process all messages in the outboxes of S_a and S_b in order. If the message is in the outbox of S_a and has final destination S_b, process the state transitions, and likewise for messages from S_b to S_a. Otherwise, if a message is in S_a and HD(S_b, msg.dest) < HD(S_a, msg.dest), move the message from the outbox of S_a to the outbox of S_b, and likewise vice versa.
- There exists a header chain keeping track of all headers, allowing all of these blocks to be merge-mined, and keeping one centralized location where the roots of each state are stored.
Essentially, instead of travelling through the hub, messages make their way around the substates along edges, and the constantly reducing Hamming distance ensures that each message always eventually gets to its destination.
The key design decision here is the arrangement of all substates into a hypercube. Why was the cube chosen? The best way to think of the cube is as a compromise between two extreme options: on the one hand the circle, and on the other hand the simplex (basically, 2N-dimensional version of a tetrahedron). In a circle, a message would need to travel on average a quarter of the way across the circle before it gets to its destination, meaning that we make no efficiency gains over the plain old hub-and-spoke model.
In a simplex, every pair of substates has an edge, so a cross-substate message would get across as soon as a block between those two substates is produced. However, with miners picking random edges it would take a long time for a block on the right edge to appear, and more importantly users watching a particular substate would need to be at least light clients on every other substate in order to validate blocks that are relevant to them. The hypercube is a perfect balance – each substate has a logarithmically growing number of neighbors, the length of the longest path grows logarithmically, and block time of any particular edge grows logarithmically.
Note that this algorithm has essentially the same flaws as the hub-and-spoke approach – namely, that it has bad degenerate-case behavior and the economics of challenge-response protocols are very unclear. To add stability, one approach is to modify the header chain somewhat.
Right now, the header chain is very strict in its validity requirements – if any block anywhere down the header chain turns out to be invalid, all blocks in all substates on top of that are invalid and must be redone. To mitigate this, we can require the header chain to simply keep track of headers, so it can contain both invalid headers and even multiple forks of the same substate chain. To add a merge-mining protocol, we implement exponential subjective scoring but using the header chain as an absolute common timekeeper. We use a low base (eg. 0.75 instead of 0.99) and have a maximum penalty factor of 1 / 2N to remove the benefit from forking the header chain; for those not well versed in the mechanics of ESS, this basically means “allow the header chain to contain all headers, but use the ordering of the header chain to penalize blocks that come later without making this penalty too strict”. Then, we add a delay on cross-substate messages, so a message in an outbox only becomes “eligible” if the originating block is at least a few dozen blocks deep.
Proof of Stake
Now, let us work on porting the protocol to nearly-pure proof of stake. We’ll ignore nothing-at-stake issues for now; Slasher-like protocols plus exponential subjective scoring can solve those concerns, and we will discuss adding them in later. Initially, our objective is to show how to make the hypercube work without mining, and at the same time partially solve the fragility problem. We will start off with a proof of activity implementation for multichain. The protocol works as follows:
- There exist 2N substates indentified by binary string, as before, as well as a header chain (which also keeps track of the latest state root of each substate).
- Anyone can mine an edge, as before, but with a lower difficulty. However, when a block is mined, it must be published alongside the complete set of Merkle tree proofs so that a node with no prior information can fully validate all state transitions in the block.
- There exists a bonding protocol where an address can specify itself as a potential signer by submitting a bond of size B (richer addresses will need to create multiple sub-accounts). Potential signers are stored in a specialized contract C[s] on each substate s.
- Based on the block hash, a random 200 substates s[i] are chosen, and a search index 0 <= ind[i] < 2^160 is chosen for each substate. Define signer[i] as the owner of the first address in C[s[i]] after index ind[i]. For the block to be valid, it must be signed by at least 133 of the set signer[0] … signer[199].
To actually check the validity of a block, the consensus group members would do two things. First, they would check that the initial state roots provided in the block match the corresponding state roots in the header chain. Second, they would process the transactions, and make sure that the final state roots match the final state roots provided in the header chain and that all trie nodes needed to calculate the update are available somewhere in the network. If both checks pass, they sign the block, and if the block is signed by sufficiently many consensus group members it gets added to the header chain, and the state roots for the two affected blocks in the header chain are updated.
And that’s all there is to it. The key property here is that every block has a randomly chosen consensus group, and that group is chosen from the global state of all account holders. Hence, unless an attacker has at least 33% of the stake in the entire system, it will be virtually impossible (specifically, 2-70 probability, which with 230 proof of work falls well into the realm of cryptographic impossiblity) for the attacker to get a block signed. And without 33% of the stake, an attacker will not be able to prevent legitimate miners from creating blocks and getting them signed.
This approach has the benefit that it has nice degenerate-case behavior; if a denial-of-service attack happens, then chances are that almost no blocks will be produced, or at least blocks will be produced very slowly, but no damage will be done.
Now, the challenge is, how do we further reduce proof of work dependence, and add in blockmaker and Slasher-based protocols? A simple approach is to have a separate blockmaker protocol for every edge, just as in the single-chain approach. To incentivize blockmakers to act honestly and not double-sign, Slasher can also be used here: if a signer signs a block that ends up not being in the main chain, they get punished. Schelling point effects ensure that everyone has the incentive to follow the protocol, as they guess that everyone else will (with the additional minor pseudo-incentive of software defaults to make the equilibrium stronger).
A full EVM
These protocols allow us to send one-way messages from one substate to another. However, one way messages are limited in functionality (or rather, they have as much functionality as we want them to have because everything is Turing-complete, but they are not always the nicest to work with). What if we can make the hypercube simulate a full cross-substate EVM, so you can even call functions that are on other substates?
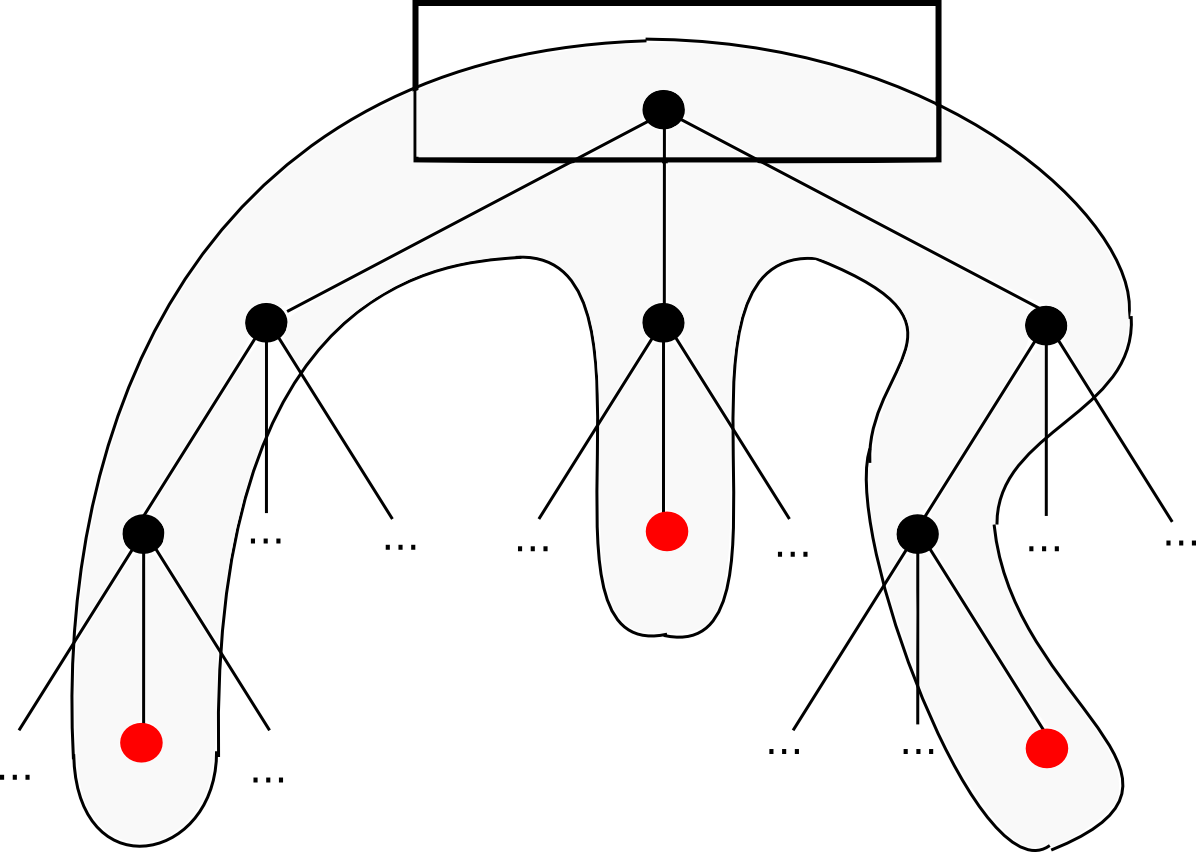
As it turns out, you can. The key is to add to messages a data structure called a continuation. For example, suppose that we are in the middle of a computation where a contract calls a contract which creates a contract, and we are currently executing the code that is creating the inner contract. Thus, the place we are in the computation looks something like this:
Now, what is the current “state” of this computation? That is, what is the set of all the data that we need to be able to pause the computation, and then using the data resume it later on? In a single instance of the EVM, that’s just the program counter (ie. where we are in the code), the memory and the stack. In a situation with contracts calling each other, we need that data for the entire “computational tree”, including where we are in the current scope, the parent scope, the parent of that, and so forth back to the original transaction:
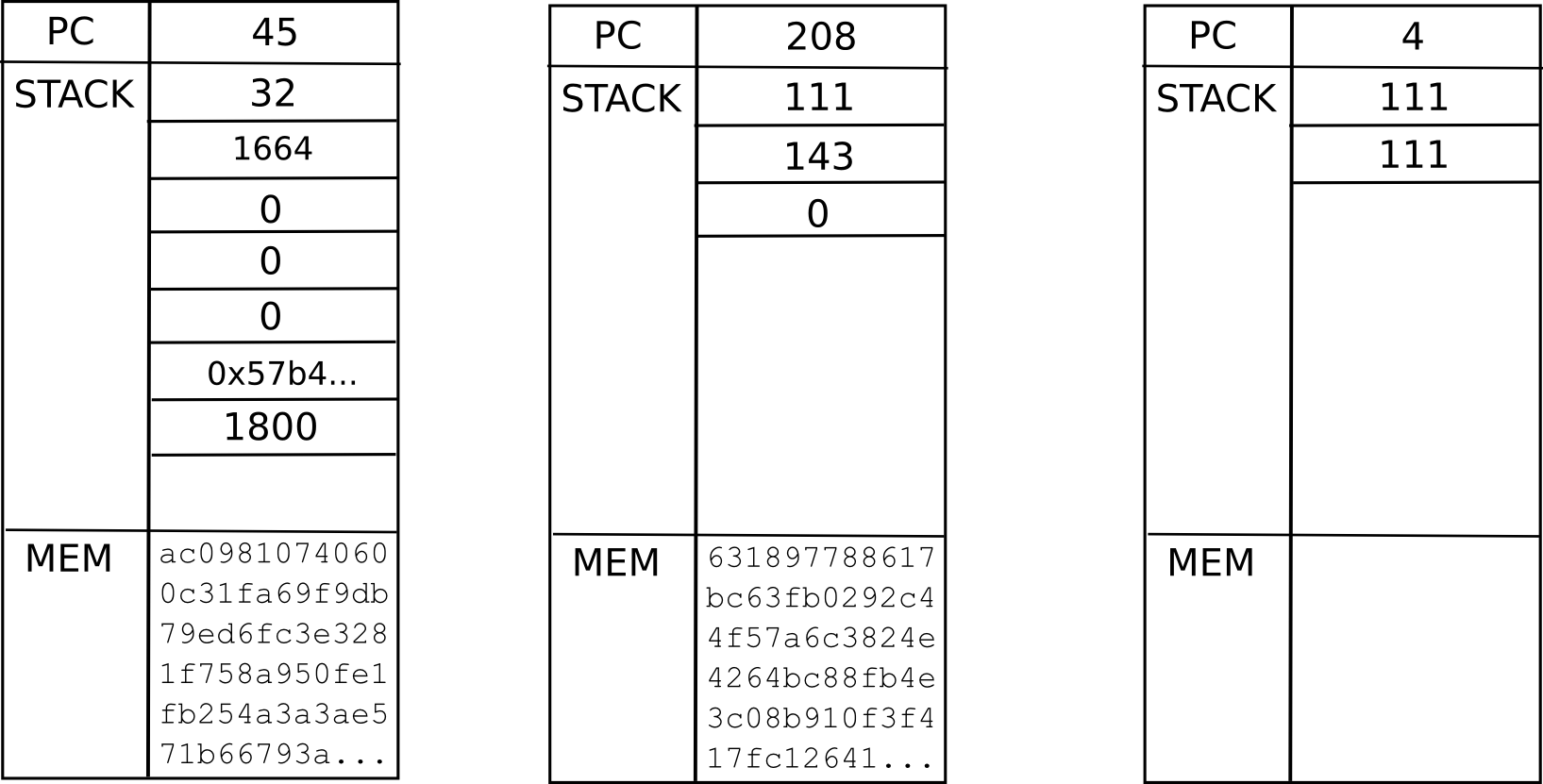
This is called a “continuation”. To resume an execution from this continuation, we simply resume each computation and run it to completion in reverse order (ie. finish the innermost first, then put its output into the appropriate space in its parent, then finish the parent, and so forth). Now, to make a fully scalable EVM, we simply replace the concept of a one-way message with a continuation, and there we go.
Of course, the question is, do we even want to go this far? First of all, going between substates, such a virtual machine would be incredibly inefficient; if a transaction execution needs to access a total of ten contracts, and each contract is in some random substate, then the process of running through that entire execution will take an average of six blocks per transmission, times two transmissions per sub-call, times ten sub-calls – a total of 120 blocks. Additionally, we lose synchronicity; if A calls B once and then again, but between the two calls C calls B, then C will have found B in a partially processed state, potentially opening up security holes. Finally, it’s difficult to combine this mechanism with the concept of reverting transaction execution if transactions run out of gas. Thus, it may be easier to not bother with continuations, and rather opt for simple one-way messages; because the language is Turing-complete continuations can always be built on top.
As a result of the inefficiency and instability of cross-chain messages no matter how they are done, most dapps will want to live entirely inside of a single sub-state, and dapps or contracts that frequently talk to each other will want to live in the same sub-state as well. To prevent absolutely everyone from living on the same sub-state, we can have the gas limits for each substate “spill over” into each other and try to remain similar across substates; then, market forces will naturally ensure that popular substates become more expensive, encouraging marginally indifferent users and dapps to populate fresh new lands.
Not So Fast
So, what problems remain? First, there is the data availability problem: what happens when all of the full nodes on a given sub-state disappear? If such a situation happens, the sub-state data disappears forever, and the blockchain will essentially need to be forked from the last block where all of the sub-state data actually is known. This will lead to double-spends, some broken dapps from duplicate messages, etc. Hence, we need to essentially be sure that such a thing will never happen. This is a 1-of-N trust model; as long as one honest node stores the data we are fine. Single-chain architectures also have this trust model, but the concern increases when the number of nodes expected to store each piece of data decreases – as it does here by a factor of 2048. The concern is mitigated by the existence of altruistic nodes including blockchain explorers, but even that will become an issue if the network scales up so much that no single data center will be able to store the entire state.
Second, there is a fragility problem: if any block anywhere in the system is mis-processed, then that could lead to ripple effects throughout the entire system. A cross-substate message might not be sent, or might be re-sent; coins might be double-spent, and so forth. Of course, once a problem is detected it would inevitably be detected, and it could be solved by reverting the whole chain from that point, but it’s entirely unclear how often such situations will arise. One fragility solution is to have a separate version of ether in each substate, allowing ethers in different substates to float against each other, and then add message redundancy features to high-level languages, accepting that messages are going to be probabilistic; this would allow the number of nodes verifying each header to shrink to something like 20, allowing even more scalability, though much of that would be absorbed by an increased number of cross-substate messages doing error-correction.
A third issue is that the scalability is limited; every transaction needs to be in a substate, and every substate needs to be in a header that every node keeps track of, so if the maximum processing power of a node is N transactions, then the network can process up to N2 transactions. An approach to add further scalability is to make the hypercube structure hierarchical in some fashion – imagine the block headers in the header chain as being transactions, and imagine the header chain itself being upgraded from a single-chain model to the exact same hypercube model as described here – that would give N3 scalability, and applying it recursively would give something very much like tree chains, with exponential scalability – at the cost of increased complexity, and making transactions that go all the way across the state space much more inefficient.
Finally, fixing the number of substates at 4096 is suboptimal; ideally, the number would grow over time as the state grew. One option is to keep track of the number of transactions per substate, and once the number of transactions per substate exceeds the number of substates we can simply add a dimension to the cube (ie. double the number of substates). More advanced approaches involve using minimal cut algorithms such as the relatively simple Karger’s algorithm to try to split each substate in half when a dimension is added. However, such approaches are problematic, both because they are complex and because they involve unexpectedly massively increasing the cost and latency of dapps that end up accidentally getting cut across the middle.
Alternative Approaches
Of course, hypercubing the blockchain is not the only approach to making the blockchain scale. One very promising alternative is to have an ecosystem of multiple blockchains, some application-specific and some Ethereum-like generalized scripting environments, and have them “talk to” each other in some fashion – in practice, this generally means having all (or at least some) of the blockchains maintain “light clients” of each other inside of their own states. The challenge there is figuring out how to have all of these chains share consensus, particularly in a proof-of-stake context. Ideally, all of the chains involved in such a system would reinforce each other, but how would one do that when one can’t determine how valuable each coin is? If an attacker has 5% of all A-coins, 3% of all B-coins and 80% of all C-coins, how does A-coin know whether it’s B-coin or C-coin that should have the greater weight?
One approach is to use what is essentially Ripple consensus between chains – have each chain decide, either initially on launch or over time via stakeholder consensus, how much it values the consensus input of each other chain, and then allow transitivity effects to ensure that each chain protects every other chain over time. Such a system works very well, as it’s open to innovation – anyone can create new chains at any point with arbitrarily rules, and all the chains can still fit together to reinforce each other; quite likely, in the future we may see such an inter-chain mechanism existing between most chains, and some large chains, perhaps including older ones like Bitcoin and architectures like a hypercube-based Ethereum 2.0, resting on their own simply for historical reasons. The idea here is for a truly decentralized design: everyone reinforces each other, rather than simply hugging the strongest chain and hoping that that does not fall prey to a black swan attack.

Leave a Reply