
Special thanks to Vlad Zamfir and Zack Hess for ongoing research and discussions on proof-of-stake algorithms and their own input into Slasher-like proposals
One of the hardest problems in cryptocurrency development is that of devising effective consensus algorithms. Certainly, relatively passable default options exist. At the very least it is possible to rely on a Bitcoin-like proof of work algorithm based on either a randomly-generated circuit approach targeted for specialized-hardware resitance, or failing that simple SHA3, and our existing GHOST optimizations allow for such an algorithm to provide block times of 12 seconds. However, proof of work as a general category has many flaws that call into question its sustainability as an exclusive source of consensus; 51% attacks from altcoin miners, eventual ASIC dominance and high energy inefficiency are perhaps the most prominent. Over the last few months we have become more and more convinced that some inclusion of proof of stake is a necessary component for long-term sustainability; however, actually implementing a proof of stake algorithm that is effective is proving to be surprisingly complex.
The fact that Ethereum includes a Turing-complete contracting system complicates things further, as it makes certain kinds of collusion much easier without requiring trust, and creates a large pool of stake in the hands of decentralized entities that have the incentive to vote with the stake to collect rewards, but which are too stupid to tell good blockchains from bad. What the rest of this article will show is a set of strategies that deal with most of the issues surrounding proof of stake algorithms as they exist today, and a sketch of how to extend our current preferred proof-of-stake algorithm, Slasher, into something much more robust.
Historical Overview: Proof of stake and Slasher
If you’re not yet well-versed in the nuances of proof of stake algorithms, first read: https://blog.ethereum.org/2014/07/05/stake/
The fundamental problem that consensus protocols try to solve is that of creating a mechanism for growing a blockchain over time in a decentralized way that cannot easily be subverted by attackers. If a blockchain does not use a consensus protocol to regulate block creation, and simply allows anyone to add a block at any time, then an attacker or botnet with very many IP addresses could flood the network with blocks, and particularly they can use their power to perform double-spend attacks – sending a payment for a product, waiting for the payment to be confirmed in the blockchain, and then starting their own “fork” of the blockchain, substituting the payment that they made earlier with a payment to a different account controlled by themselves, and growing it longer than the original so everyone accepts this new blockchain without the payment as truth.
The general solution to this problem involves making a block “hard” to create in some fashion. In the case of proof of work, each block requires computational effort to produce, and in the case of proof of stake it requires ownership of coins – in most cases, it’s a probabilistic process where block-making privileges are doled out randomly in proportion to coin holdings, and in more exotic “negative block reward” schemes anyone can create a block by spending a certain quantity of funds, and they are compensated via transaction fees. In any of these approaches, each chain has a “score” that roughly reflects the total difficulty of producing the chain, and the highest-scoring chain is taken to represent the “truth” at that particular time.
For a detailed overview of some of the finer points of proof of stake, see the above-linked article; for those readers who are already aware of the issues I will start off by presenting a semi-formal specification for Slasher:
- Blocks are produced by miners; in order for a block to be valid it must satisfy a proof-of-work condition. However, this condition is relatively weak (eg. we can target the mining reward to something like 0.02x the genesis supply every year)
- Every block has a set of designated signers, which are chosen beforehand (see below). For a block with valid PoW to be accepted as part of the chain it must be accompanied by signatures from at least two thirds of its designated signers.
- When block N is produced, we say that the set of potential signers of block N + 3000 is the set of addresses such that sha3(address + block[N].hash) < block[N].balance(address) * D2 where D2 is a difficulty parameter targeting 15 signers per block (ie. if block N has less than 15 signers it goes down otherwise it goes up). Note that the set of potential signers is very computationally intensive to fully enumerate, and we don’t try to do so; instead we rely on signers to self-declare.
- If a potential signer for block N + 3000 wants to become a designated signer for that block, they must send a special transaction accepting this responsibility and that transaction must get included between blocks N + 1 and N + 64. The set of designated signers for block N + 3000 is the set of all individuals that do this. This “signer must confirm” mechanism helps ensure that the majority of signers will actually be online when the time comes to sign. For blocks 0 … 2999, the set of signers is empty, so proof of work alone suffices to create those blocks.
- When a designated signer adds their signature to block N + 3000, they are scheduled to receive a reward in block N + 6000.
- If a signer signs two different blocks at height N + 3000, then if someone detects the double-signing before block N + 6000 they can submit an “evidence” transaction containing the two signatures, destroying the signer’s reward and transferring a third of it to the whistleblower.
- If there is an insufficient number of signers to sign at a particular block height h, a miner can produce a block with height h+1 directly on top of the block with height h-1 by mining at an 8x higher difficulty (to incentivize this, but still make it less attractive than trying to create a normal block, there is a 6x higher reward). Skipping over two blocks has higher factors of 16x diff and 12x reward, three blocks 32x and 24x, etc.
Essentially, by explicitly punishing double-signing, Slasher in a lot of ways, although not all, makes proof of stake act like a sort of simulated proof of work. An important incidental benefit of Slasher is the non-revert property. In proof of work, sometimes after one node mines one block some other node will immediately mine two blocks, and so some nodes will need to revert back one block upon seeing the longer chain. Here, every block requires two thirds of the signers to ratify it, and a signer cannot ratify two blocks at the same height without losing their gains in both chains, so assuming no malfeasance the blockchain will never revert. From the point of view of a decentralized application developer, this is a very desirable property as it means that “time” only moves in one direction, just like in a server-based environment.
However, Slasher is still vulnerable to one particular class of attack: long-range attacks. Instead of trying to start a fork from ten blocks behind the current head, suppose that an attacker tries to start a fork starting from ten thousand blocks behind, or even the genesis block – all that matters is that the depth of the fork must be greater than the duration of the reward lockup. At that point, because users’ funds are unlocked and they can move them to a new address to escape punishment, users have no disincentive against signing on both chains. In fact, we may even expect to see a black market of people selling their old private keys, culminating with an attacker single-handedly acquiring access to the keys that controlled over 50% of the currency supply at some point in history.
One approach to solving the long-range double-signing problem is transactions-as-proof-of-stake, an alternative PoS solution that does not have an incentive to double-sign because it’s the transactions that vote, and there is no reward for sending a transaction (in fact there’s a cost, and the reward is outside the network); however, this does nothing to stop the black key market problem. To properly deal with that issue, we will need to relax a hidden assumption.
Subjective Scoring and Trust
For all its faults, proof of work does have some elegant economic properties. Particularly, because proof of work requires an externally rivalrous resource, something with exists and is consumed outside the blockchain, in order to generate blocks (namely, computational effort), launching a fork against a proof of work chain invariably requires having access to, and spending, a large quantity of economic resources. In the case of proof of stake, on the other hand, the only scarce value involved is value within the chain, and between multiple chains that value is not scarce at all. No matter what algorithm is used, in proof of stake 51% of the owners of the genesis block could eventually come together, collude, and produce a longer (ie. higher-scoring) chain than everyone else.
This may seem like a fatal flaw, but in reality it is only a flaw if we implicitly accept an assumption that is made in the case of proof of work: that nodes have no knowledge of history. In a proof-of-work protocol, a new node, having no direct knowledge of past events and seeing nothing but the protocol source code and the set of messages that have already been published, can join the network at any point and determine the score of all possible chains, and from there the block that is at the top of the highest-scoring main chain. With proof of stake, as we described, such a property cannot be achieved, since it’s very cheap to acquire historical keys and simulate alternate histories. Thus, we will relax our assumptions somewhat: we will say that we are only concerned with maintaining consensus between a static set of nodes that are online at least once every N days, allowing these nodes to use their own knowledge of history to reject obvious long-range forks using some formula, and new nodes or long-dormant nodes will need to specify a “checkpoint” (a hash of a block representing what the rest of the network agrees is a recent state) in order to get back onto the consensus.
Such an approach is essentially a hybrid between the pure and perhaps harsh trust-no-one logic of Bitcoin and the total dependency on socially-driven consensus found in networks like Ripple. In Ripple’s case, users joining the system need to select a set of nodes that they trust (or, more precisely, trust not to collude) and rely on those nodes during every step of the consensus process. In the case of Bitcoin, the theory is that no such trust is required and the protocol is completely self-contained; the system works just as well between a thousand isolated cavemen with laptops on a thousand islands as it does in a strongly connected society (in fact, it might work better with island cavemen, since without trust collusion is more difficult). In our hybrid scheme, users need only look to the society outside of the protocol exactly once – when they first download a client and find a checkpoint – and can enjoy Bitcoin-like trust properties starting from that point.
In order to determine which trust assumption is the better one to take, we ultimately need to ask a somewhat philosophical question: do we want our consensus protocols to exist as absolute cryptoeconomic constructs completely independent of the outside world, or are we okay with relying heavily on the fact that these systems exist in the context of a wider society? Although it is indeed a central tenet of mainstream cryptocurrency philosophy that too much external dependence is dangerous, arguably the level of independence that Bitcoin affords us in reality is no greater than that provided by the hybrid model. The argument is simple: even in the case of Bitcoin, a user must also take a leap of trust upon joining the network – first by trusting that they are joining a protocol that contains assets that other people find valuable (eg. how does a user know that bitcoins are worth $380 each and dogecoins only $0.0004? Especially with the different capabilities of ASICs for different algorithms, hashpower is only a very rough estimate), and second by trusting that they are downloading the correct software package. In both the supposedly “pure” model and the hybrid model there is always a need to look outside the protocol exactly once. Thus, on the whole, the gain from accepting the extra trust requirement (namely, environmental friendliness and security against oligopolistic mining pools and ASIC farms) is arguably worth the cost.
Additionally, we may note that, unlike Ripple consensus, the hybrid model is still compatible with the idea of blockchains “talking” to each each other by containing a minimal “light” implementation of each other’s protocols. The reason is that, while the scoring mechanism is not “absolute” from the point of view of a node without history suddenly looking at every block, it is perfectly sufficient from the point of view of an entity that remains online over a long period of time, and a blockchain certainly is such an entity.
So far, there have been two major approaches that followed some kind of checkpoint-based trust model:
- Developer-issued checkpoints – the client developer issues a new checkpoint with each client upgrade (eg. used in PPCoin)
- Revert limit – nodes refuse to accept forks that revert more than N (eg. 3000) blocks (eg. used in Tendermint)
The first approach has been roundly criticized by the cryptocurrency community for being too centralized. The second, however, also has a flaw: a powerful attacker can not only revert a few thousand blocks, but also potentially split the network permanently. In the N-block revert case, the strategy is as follows. Suppose that the network is currently at block 10000, and N = 3000. The attacker starts a secret fork, and grows it by 3001 blocks faster than the main network. When the main network gets to 12999, and some node produces block 13000, the attacker reveals his own fork. Some nodes will see the main network’s block 13000, and refuse to switch to the attacker’s fork, but the nodes that did not yet see that block will be happy to revert from 12999 to 10000 and then accept the attacker’s fork. From there, the network is permanently split.
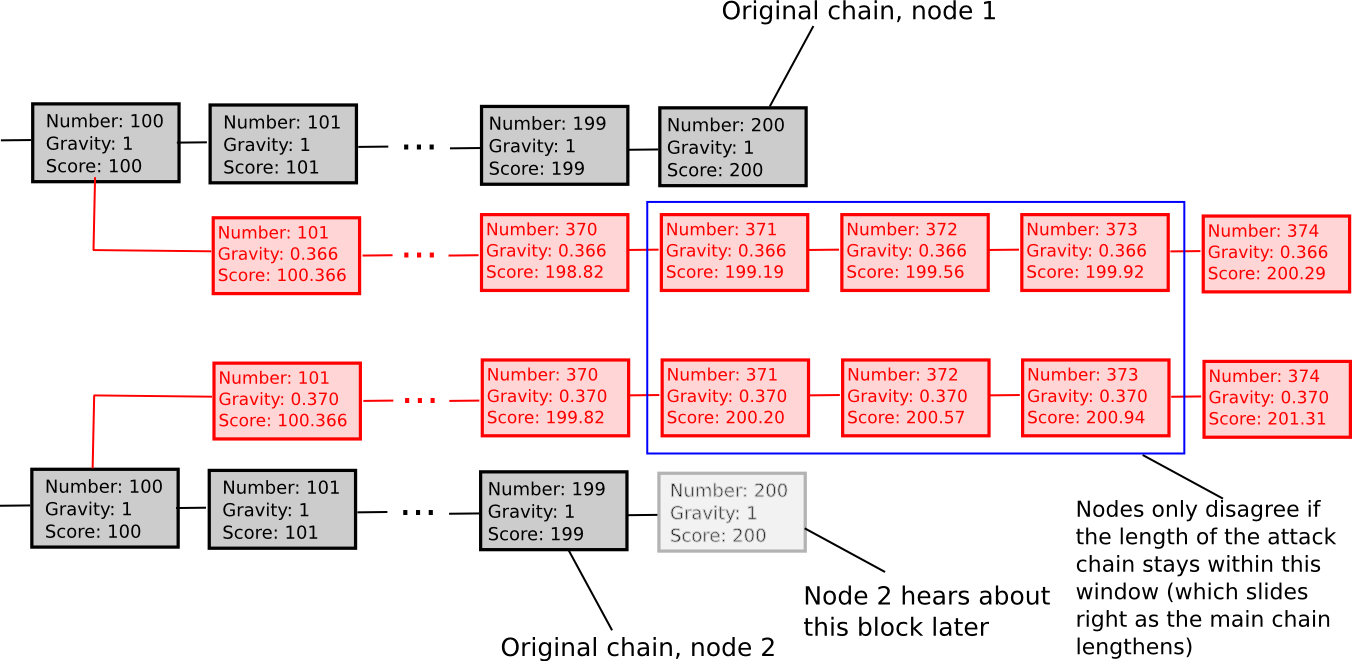
Fortunately, one can actually construct a third approach that neatly solves this problem, which we will call exponentially subjective scoring. Essentially, instead of rejecting forks that go back too far, we simply penalize them on a graduating scale. For every block, a node maintains a score and a “gravity” factor, which acts as a multiplier to the contribution that the block makes to the blockchain’s score. The gravity of the genesis block is 1, and normally the gravity of any other block is set to be equal to the gravity of its parent. However, if a node receives a block whose parent already has a chain of N descendants (ie. it’s a fork reverting N blocks), that block’s gravity is penalized by a factor of 0.99N, and the penalty propagates forever down the chain and stacks multiplicatively with other penalties.
That is, a fork which starts 1 block ago will need to grow 1% faster than the main chain in order to overtake it, a fork which starts 100 blocks ago will need to grow 2.718 times as quickly, and a fork which starts 3000 blocks ago will need to grow 12428428189813 times as quickly – clearly an impossibility with even trivial proof of work.
The algorithm serves to smooth out the role of checkpointing, assigning a small “weak checkpoint” role to each individual block. If an attacker produces a fork that some nodes hear about even three blocks earlier than others, those two chains will need to stay within 3% of each other forever in order for a network split to maintain itself.
There are other solutions that could be used aside from, or even alongside ESS; a particular set of strategies involves stakeholders voting on a checkpoint every few thousand blocks, requiring every checkpoint produced to reflect a large consensus of the majority of the current stake (the reason the majority of the stake can’t vote on every block is, of course, that having that many signatures would bloat the blockchain).
Slasher Ghost
The other large complexity in implementing proof of stake for Ethereum specifically is the fact that the network includes a Turing-complete financial system where accounts can have arbitrary permissions and even permissions that change over time. In a simple currency, proof of stake is relatively easy to accomplish because each unit of currency has an unambiguous owner outside the system, and that owner can be counted on to participate in the stake-voting process by signing a message with the private key that owns the coins. In Ethereum, however, things are not quite so simple: if we do our job promoting proper wallet security right, the majority of ether is going to be stored in specialized storage contracts, and with Turing-complete code there is no clear way of ascertaining or assigning an “owner”.
One strategy that we looked at was delegation: requiring every address or contract to assign an address as a delegate to sign for them, and that delegate account would have to be controlled by a private key. However, there is a problem with any such approach. Suppose that a majority of the ether in the system is actually stored in application contracts (as opposed to personal storage contracts); this includes deposits in SchellingCoins and other stake-based protocols, security deposits in probabilistic enforcement systems, collateral for financial derivatives, funds owned by DAOs, etc. Those contracts do not have an owner even in spirit; in that case, the fear is that the contract will default to a strategy of renting out stake-voting delegations to the highest bidder. Because attackers are the only entities willing to bid more than the expected return from the delegation, this will make it very cheap for an attacker to acquire the signing rights to large quantities of stake.
The only solution to this within the delegation paradigm is to make it extremely risky to dole out signing privileges to untrusted parties; the simplest approach is to modify Slasher to require a large deposit, and slash the deposit as well as the reward in the event of double-signing. However, if we do this then we are essentially back to entrusting the fate of a large quantity of funds to a single private key, thereby defeating much of the point of Ethereum in the first place.
Fortunately, there is one alternative to delegation that is somewhat more effective: letting contracts themselves sign. To see how this works, consider the following protocol:
- There is now a SIGN opcode added.
- A signature is a series of virtual transactions which, when sequentially applied to the state at the end of the parent block, results in the SIGN opcode being called. The nonce of the first VTX in the signature must be the prevhash being signed, the nonce of the second must be the prevhash plus one, and so forth (alternatively, we can make the nonces -1, -2, -3 etc. and require the prevhash to be passed in through transaction data so as to be eventually supplied as an input to the SIGN opcode).
- When the block is processed, the state transitions from the VTXs are reverted (this is what is meant by “virtual”) but a deposit is subtracted from each signing contract and the contract is registered to receive the deposit and reward in 3000 blocks.
Basically, it is the contract’s job to determine the access policy for signing, and the contract does this by placing the SIGN opcode behind the appropriate set of conditional clauses. A signature now becomes a set of transactions which together satisfy this access policy. The incentive for contract developers to keep this policy secure, and not dole it out to anyone who asks, is that if it is not secure then someone can double-sign with it and destroy the signing deposit, taking a portion for themselves as per the Slasher protocol. Some contracts will still delegate, but this is unavoidable; even in proof-of-stake systems for plain currencies such as NXT, many users end up delegating (eg. DPOS even goes so far as to institutionalize delegation), and at least here contracts have an incentive to delegate to an access policy that is not likely to come under the influence of a hostile entity – in fact, we may even see an equilibrium where contracts compete to deliver secure blockchain-based stake pools that are least likely to double-vote, thereby increasing security over time.
However, the virtual-transactions-as-signatures paradigm does impose one complication: it is no longer trivial to provide an evidence transaction showing two signatures by the same signer at the same block height. Because the result of a transaction execution depends on the starting state, in order to ascertain whether a given evidence transaction is valid one must prove everything up to the block in which the second signature was given. Thus, one must essentially “include” the fork of a blockchain inside of the main chain. To do this efficiently, a relatively simple proposal is a sort of “Slasher GHOST” protocol, where one can include side-blocks in the main chain as uncles. Specifically, we declare two new transaction types:
- [block_number, uncle_hash] – this transaction is valid if (1) the block with the given uncle_hash has already been validated, (2) the block with the given uncle_hash has the given block number, and (3) the parent of that uncle is either in the main chain or was included earlier as an uncle. During the act of processing this transaction, if addresses that double-signed at that height are detected, they are appropriately penalized.
- [block_number, uncle_parent_hash, vtx] – this transaction is valid if (1) the block with the given uncle_parent_hash has already been validated, (2) the given virtual transaction is valid at the given block height with the state at the end of uncle_parent_hash, and (3) the virtual transaction shows a signature by an address which also signed a block at the given block_number in the main chain. This transaction penalizes that one address.

Essentially, one can think of the mechanism as working like a “zipper”, with one block from the fork chain at a time being zipped into the main chain. Note that for a fork to start, there must exist double-signers at every block; there is no situation where there is a double-signer 1500 blocks into a fork so a whistleblower must “zip” 1499 innocent blocks into a chain before getting to the target block – rather, in such a case, even if 1500 blocks need to be added, each one of them notifies the main chain about five separate malfeasors that double-signed at that height. One somewhat complicated property of the scheme is that the validity of these “Slasher uncles” depends on whether or not the node has validated a particular block outside of the main chain; to facilitate this, we specify that a response to a “getblock” message in the wire protocol must include the uncle-dependencies for a block before the actual block. Note that this may sometimes lead to a recursive expansion; however, the denial-of-service potential is limited since each individual block still requires a substantial quantity of proof-of-work to produce.
Blockmakers and Overrides
Finally, there is a third complication. In the hybrid-proof-of-stake version of Slasher, if a miner has an overwhelming share of the hashpower, then the miner can produce multiple versions of each block, and send different versions to different parts of the network. Half the signers will see and sign one block, half will see and sign another block, and the network will be stuck with two blocks with insufficient signatures, and no signer willing to slash themselves to complete the process; thus, a proof-of-work override will be required, a dangerous situation since the miner controls most of the proof-of-work. There are two possible solutions here:
- Signers should wait a few seconds after receiving a block before signing, and only sign stochastically in some fashion that ensures that a random one of the blocks will dominate.
- There should be a single “blockmaker” among the signers whose signature is required for a block to be valid. Effectively, this transfers the “leadership” role from a miner to a stakeholder, eliminating the problem, but at the cost of adding a dependency on a single party that now has the ability to substantially inconvenience everyone by not signing, or unintentionally by being the target of a denial-of-service attack. Such behavior can be disincentivized by having the signer lose part of their deposit if they do not sign, but even still this will result in a rather jumpy block time if the only way to get around an absent blockmaker is using a proof-of-work override.
One possible solution to the problem in (2) is to remove proof of work entirely (or almost entirely, keeping a minimal amount for anti-DDoS value), replacing it with a mechanism that Vlad Zamfir has coined “delegated timestamping”. Essentially, every block must appear on schedule (eg. at 15 second intervals), and when a block appears the signers vote 1 if the block was on time, or 0 if the block was too early or too late. If the majority of the signers votes 0, then the block is treated as invalid – kept in the chain in order to give the signers their fair reward, but the blockmaker gets no reward and the state transition gets skipped over. Voting is incentivized via schellingcoin – the signers whose vote agrees with the majority get an extra reward, so assuming that everyone else is going to be honest everyone has the incentive to be honest, in a self-reinforcing equilibrium. The theory is that a 15-second block time is too fast for signers to coordinate on a false vote (the astute reader may note that the signers were decided 3000 blocks in advance so this is not really true; to fix this we can create two groups of signers, one pre-chosen group for validation and another group chosen at block creation time for timestamp voting).
Putting it all Together
Taken together, we can thus see something like the following working as a functional version of Slasher:
- Every block has a designated blockmaker, a set of designated signers, and a set of designated timestampers. For a block to be accepted as part of the chain it must be accompanied by virtual-transactions-as-signatures from the blockmaker, two thirds of the signers and 10 timestampers, and the block must have some minimal proof of work for anti-DDoS reasons (say, targeted to 0.01x per year)
- During block N, we say that the set of potential signers of block N + 3000 is the set of addresses such that sha3(address + block[N].hash) < block[N].balance(address) * D2 where D2 is a difficulty parameter targeting 15 signers per block (ie. if block N has less than 15 signers it goes down otherwise it goes up).
- If a potential signer for block N + 3000 wants to become a signer, they must send a special transaction accepting this responsibility and supplying a deposit, and that transaction must get included between blocks N + 1 and N + 64. The set of designated signers for block N + 3000 is the set of all individuals that do this, and the blockmaker is the designated signer with the lowest value for sha3(address + block[N].hash). If the signer set is empty, no block at that height can be made. For blocks 0 … 2999, the blockmaker and only signer is the protocol developer.
- The set of timestampers of the block N + 3000 is the set of addresses such that sha3(address + block[N].hash) < block[N].balance(address) * D3, where D3 is targeted such that there is an average of 20 timestampers each block (ie. if block N has less than 20 timestampers it goes down otherwise it goes up).
- Let T be the timestamp of the genesis block. When block N + 3000 is released, timestampers can supply virtual-transactions-as-signatures for that block, and have the choice of voting 0 or 1 on the block. Voting 1 means that they saw the block within 7.5 seconds of time T + (N + 3000) * 15, and voting 0 means that they received the block when the time was outside that range. Note that nodes should detect if their clocks are out of sync with everyone else’s clocks on the blockchain, and if so adjust their system clocks.
- Timestampers who voted along with the majority receive a reward, other timestampers get nothing.
- The designated signers for block N + 3000 have the ability to sign that block by supplying a set of virtual-transactions-as-a-signature. All designated signers who sign are scheduled to receive a reward and their returned deposit in block N + 6000. Signers who skipped out are scheduled to receive their returned deposit minus twice the reward (this means that it’s only economically profitable to sign up as a signer if you actually think there is a chance greater than 2/3 that you will be online).
- If the majority timestamper vote is 1, the blockmaker is scheduled to receive a reward and their returned deposit in block N + 6000. If the majority timestamper vote is 0, the blockmaker is scheduled to receive their deposit minus twice the reward, and the block is ignored (ie. the block is in the chain, but it does not contribute to the chain’s score, and the state of the next block starts from the end state of the block before the rejected block).
- If a signer signs two different blocks at height N + 3000, then if someone detects the double-signing before block N + 6000 they can submit an “evidence” transaction containing the two signatures to either or both chains, destroying the signer’s reward and deposit and transferring a third of it to the whistleblower.
- If there is an insufficient number of signers to sign or the blockmaker is missing at a particular block height h, the designated blockmaker for height h + 1 can produce a block directly on top of the block at height h – 1 after waiting for 30 seconds instead of 15.
After years of research, one thing has become clear: proof of stake is non-trivial – so non-trivial that some even consider it impossible. The issues of nothing-at-stake and long-range attacks, and the lack of mining as a rate-limiting device, require a number of compensatory mechanisms, and even the protocol above does not address the issue of how to randomly select signers. With a substantial proof of work reward, the problem is limited, as block hashes can be a source of randomness and we can mathematically show that the gain from holding back block hashes until a miner finds a hash that favorably selects future signers is usually less than the gain from publishing the block hashes. Without such a reward, however, other sources of randomness such as low-influence functions need to be used.
For Ethereum 1.0, we consider it highly desirable to both not excessively delay the release and not try too many untested features at once; hence, we will likely stick with ASIC-resistant proof of work, perhaps with non-Slasher proof of activity as an addon, and look at moving to a more comprehensive proof of stake model over time.

Leave a Reply