
The primary expense that must be paid by a blockchain is that of security. The blockchain must pay miners or validators to economically participate in its consensus protocol, whether proof of work or proof of stake, and this inevitably incurs some cost. There are two ways to pay for this cost: inflation and transaction fees. Currently, Bitcoin and Ethereum, the two leading proof-of-work blockchains, both use high levels of inflation to pay for security; the Bitcoin community presently intends to decrease the inflation over time and eventually switch to a transaction-fee-only model. NXT, one of the larger proof-of-stake blockchains, pays for security entirely with transaction fees, and in fact has negative net inflation because some on-chain features require destroying NXT; the current supply is 0.1% lower than the original 1 billion. The question is, how much “defense spending” is required for a blockchain to be secure, and given a particular amount of spending required, which is the best way to get it?
Absolute size of PoW / PoS Rewards
To provide some empirical data for the next section, let us consider bitcoin as an example. Over the past few years, bitcoin transaction revenues have been in the range of 15-75 BTC per day, or about 0.35 BTC per block (or 1.4% of current mining rewards), and this has remained true throughout large changes in the level of adoption.
It is not difficult to see why this may be the case: increases in BTC adoption will increase the total sum of USD-denominated fees (whether through transaction volume increases or average fee increases or a combination of both) but also decrease the amount of BTC in a given quantity of USD, so it is entirely reasonable that, absent exogenous block size crises, changes in adoption that do not come with changes to underlying market structure will simply leave the BTC-denominanted total transaction fee levels largely unchanged.
In 25 years, bitcoin mining rewards are going to almost disappear; hence, the 0.35 BTC per block will be the only source of revenue. At today’s prices, this works out to ~$35000 per day or $10 million per year. We can estimate the cost of buying up enough mining power to take over the network given these conditions in several ways.
First, we can look at the network hashpower and the cost of consumer miners. The network currently has 1471723 TH/s of hashpower, the best available miners cost $100 per 1 TH/s, so buying enough of these miners to overwhelm the existing network will cost ~$147 million USD. If we take away mining rewards, revenues will decrease by a factor of 36, so the mining ecosystem will in the long term decrease by a factor of 36, so the cost becomes $4.08m USD. Note that this is if you are buying new miners; if you are willing to buy existing miners, then you need to only buy half the network, knocking the cost of what Tim Swanson calls a “Maginot line” attack all the way down to ~$2.04m USD.
However, professional mining farms are likely able to obtain miners at substantially cheaper than consumer costs. We can look at the available information on Bitfury’s $100 million data center, which is expected to consume 100 MW of electricity. The farm will contain a combination of 28nm and 16nm chips; the 16nm chips “achieve energy efficiency of 0.06 joules per gigahash”. Since we care about determining the cost for a new attacker, we will assume that an attacker replicating Bitfury’s feat will use 16nm chips exclusively. 100 MW at 0.06 joules per gigahash (physics reminder: 1 joule per GH = 1 watt per GH/sec) is 1.67 billion GH/s, or 1.67M TH/s. Hence, Bitfury was able to do $60 per TH/s, a statistic that would give a $2.45m cost of attacking “from outside” and a $1.22m cost from buying existing miners.
Hence, we have $1.2-4m as an approximate estimate for a “Maginot line attack” against a fee-only network. Cheaper attacks (eg. “renting” hardware) may cost 10-100 times less. If the bitcoin ecosystem increases in size, then this value will of course increase, but then the size of transactions conducted over the network will also increase and so the incentive to attack will also increase. Is this level of security enough in order to secure the blockchain against attacks? It is hard to tell; it is my own opinion that the risk is very high that this is insufficient and so it is dangerous for a blockchain protocol to commit itself to this level of security with no way of increasing it (note that Ethereum’s current proof of work carries no fundamental improvements to Bitcoin’s in this regard; this is why I personally have not been willing to commit to an ether supply cap at this point).
In a proof of stake context, security is likely to be substantially higher. To see why, note that the ratio between the computed cost of taking over the bitcoin network, and the annual mining revenue ($932 million at current BTC price levels), is extremely low: the capital costs are only worth about two months of revenue. In a proof of stake context, the cost of deposits should be equal to the infinite future discounted sum of the returns; that is, assuming a risk-adjusted discount rate of, say, 5%, the capital costs are worth 20 years of revenue. Note that if ASIC miners consumed no electricity and lasted forever, the equilibrium in proof of work would be the same (with the exception that proof of work would still be more “wasteful” than proof of stake in an economic sense, and recovery from successful attacks would be harder); however, because electricity and especially hardware depreciation do make up the great bulk of the costs of ASIC mining, the large discrepancy exists. Hence, with proof of stake, we may see an attack cost of $20-100 million for a network the size of Bitcoin; hence it is more likely that the level of security will be enough, but still not certain.
The Ramsey Problem
Let us suppose that relying purely on current transaction fees is insufficient to secure the network. There are two ways to raise more revenue. One is to increase transaction fees by constraining supply to below efficient levels, and the other is to add inflation. How do we choose which one, or what proportions of both, to use?
Fortunately, there is an established rule in economics for solving the problem in a way that minimizes economic deadweight loss, known as Ramsey pricing. Ramsey’s original scenario was as follows. Suppose that there is a regulated monopoly that has the requirement to achieve a particular profit target (possibly to break even after paying fixed costs), and competitive pricing (ie. where the price of a good was set to equal the marginal cost of producing one more unit of the good) would not be sufficient to achieve that requirement. The Ramsey rule says that markup should be inversely proportional to demand elasticity, ie. if a 1% increase in price in good A causes a 2% reduction in demand, whereas a 1% increase in price in good B causes a 4% reduction in demand, then the socially optimal thing to do is to have the markup on good A be twice as high as the markup on good B (you may notice that this essentially decreases demand uniformly).
The reason why this kind of balanced approach is taken, rather than just putting the entire markup on the most inelastic part of the demand, is that the harm from charging prices above marginal cost goes up with the square of the markup. Suppose that a given item takes $20 to produce, and you charge $21. There are likely a few people who value the item at somewhere between $20 and $21 (we’ll say average of $20.5), and it is a tragic loss to society that these people will not be able to buy the item even though they would gain more from having it than the seller would lose from giving it up. However, the number of people is small and the net loss (average $0.5) is small. Now, suppose that you charge $30. There are now likely ten times more people with “reserve prices” between $20 and $30, and their average valuation is likely around $25; hence, there are ten times more people who suffer, and the average social loss from each one of them is now $5 instead of $0.5, and so the net social loss is 100x greater. Because of this superlinear growth, taking a little from everyone is less bad than taking a lot from one small group.

Notice how the “deadweight loss” section is a triangle. As you (hopefully) remember from math class, the area of a triangle is width * length / 2, so doubling the dimensions quadruples the area.
In Bitcoin’s case, right now we see that transaction fees are and consistently have been in the neighborhood of ~50 BTC per day, or ~18000 BTC per year, which is ~0.1% of the coin supply. We can estimate as a first approximation that, say, a 2x fee increase would reduce transaction load by 20%. In practice, it seems like bitcoin fees are up ~2x since a year ago and it seems plausible that transaction load is now ~20% stunted compared to what it would be without the fee increase (see this rough projection); these estimates are highly unscientific but they are a decent first approximation.
Now, suppose that 0.5% annual inflation would reduce interest in holding BTC by perhaps 10%, but we’ll conservatively say 25%. If at some point the Bitcoin community decides that it wants to increase security expenditures by ~200,000 BTC per year, then under those estimates, and assuming that current txfees are optimal before taking into account security expenditure considerations, the optimum would be to push up fees by 2.96x and introduce 0.784% annual inflation. Other estimates of these measures would give other results, but in any case the optimal level of both the fee increase and the inflation would be nonzero. I use Bitcoin as an example because it is the one case where we can actually try to observe the effects of growing usage restrained by a fixed cap, but identical arguments apply to Ethereum as well.
Game-Theoretic Attacks
There is also another argument to bolster the case for inflation. This is that relying on transaction fees too much opens up the playing field for a very large and difficult-to-analyze category of game-theoretic attacks. The fundamental cause is simple: if you act in a way that prevents another block from getting into the chain, then you can steal that block’s transactions. Hence there is an incentive for a validator to not just help themselves, but also to hurt others. This is even more direct than selfish-mining attacks, as in the case of selfish mining you hurt a specific validator to the benefit of all other validators, whereas here there are often opportunities for the attacker to benefit exclusively.
In proof of work, one simple attack would be that if you see a block with a high fee, you attempt to mine a sister block containing the same transactions, and then offer a bounty of 1 BTC to the next miner to mine on top of your block, so that subsequent validators have the incentive to include your block and not the original. Of course, the original miner can then follow up by increasing the bounty further, starting a bidding war, and the miner could also pre-empt such attacks by voluntarily giving up most of the fee to the creator of the next block; the end result is hard to predict and it’s not at all clear that it is anywhere close to efficient for the network. In proof of stake, similar attacks are possible.
How to distribute fees?
Even given a particular distribution of revenues from inflation and revenues from transaction fees, there is an additional choice of how the transaction fees are collected. Though most protocols so far have taken one single route, there is actually quite a bit of latitude here. The three primary choices are:
- Fees go to the validator/miner that created the block
- Fees go to the validators equally
- Fees are burned
Arguably, the more salient difference is between the first and the second; the difference between the second and the third can be described as a targeting policy choice, and so we will deal with this issue separately in a later section. The difference between the first two options is this: if the validator that creates a block gets the fees, that validator has an incentive equal to the size of the fees to include as many transactions as possible. If it’s the validators equally, each one has a negligible incentive.
Note that literally redistributing 100% of fees (or, for that matter, any fixed percentage of fees) is infeasible due to “tax evasion” attacks via side-channel payment: instead of adding a transaction fee using the standard mechanism, transaction senders will put a zero or near-zero “official fee” and pay validators directly via other cryptocurrencies (or even PayPal), allowing validators to collect 100% of the revenue. However, we can get what we want by using another trick: determine in protocol a minimum fee that transactions must pay, and have the protocol “confiscate” that portion but let the miners keep the entire excess (alternatively, miners keep all transaction fees but must in turn pay a fee per byte or unit gas to the protocol; this a mathematically equivalent formulation). This removes tax evasion incentives, while still placing a large portion of transaction fee revenue under the control of the protocol, allowing us to keep fee-based issuance without introducing the game-theoretic malicentives of a traditional pure-fee model.
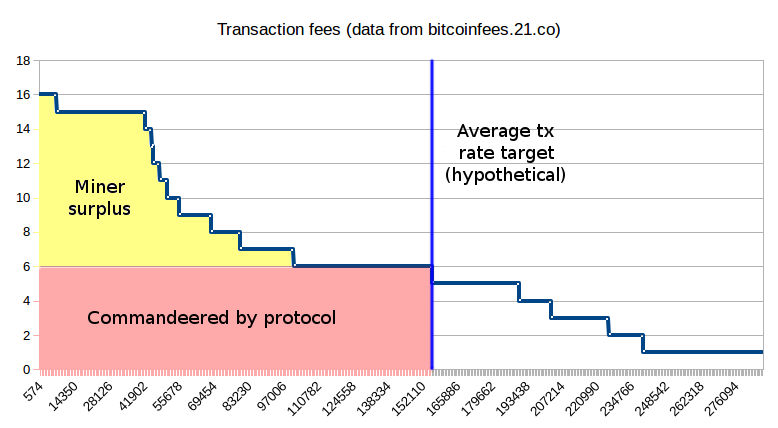
The protocol cannot take all of the transaction fee revenues because the level of fees is very uneven and because it cannot price-discriminate, but it can take a portion large enough that in-protocol mechanisms have enough revenue allocating power to work with to counteract game-theoretic concerns with traditional fee-only security.
One possible algorithm for determining this minimum fee would be a difficulty-like adjustment process that targets a medium-term average gas usage equal to 1/3 of the protocol gas limit, decreasing the minimum fee if average usage is below this value and increasing the minimum fee if average usage is higher.
We can extend this model further to provide other interesting properties. One possibility is that of a flexible gas limit: instead of a hard gas limit that blocks cannot exceed, we have a soft limit G1 and a hard limit G2 (say, G2 = 2 * G1). Suppose that the protocol fee is 20 shannon per gas (in non-Ethereum contexts, substitute other cryptocurrency units and “bytes” or other block resource limits as needed). All transactions up to G1 would have to pay 20 shannon per gas. Above that point, however, fees would increase: at (G2 + G1) / 2, the marginal unit of gas would cost 40 shannon, at (3 * G2 + G1) / 4 it would go up to 80 shannon, and so forth until hitting a limit of infinity at G2. This would give the chain a limited ability to expand capacity to meet sudden spikes in demand, reducing the price shock (a feature that some critics of the concept of a “fee market” may find attractive).
What to Target
Let us suppose that we agree with the points above. Then, a question still remains: how do we target our policy variables, and particularly inflation? Do we target a fixed level of participation in proof of stake (eg. 30% of all ether), and adjust interest rates to compensate? Do we target a fixed level of total inflation? Or do we just set a fixed interest rate, and allow participation and inflation to adjust? Or do we take some middle road where greater interest in participating leads to a combination of increased inflation, increased participation and a lower interest rate?
In general, tradeoffs between targeting rules are fundamentally tradeoffs about what kinds of uncertainty we are more willing to accept, and what variables we want to reduce volatility on. The main reason to target a fixed level of participation is to have certainty about the level of security. The main reason to target a fixed level of inflation is to satisfy the demands of some token holders for supply predictability, and at the same time have a weaker but still present guarantee about security (it is theoretically possible that in equilibrium only 5% of ether would be participating, but in that case it would be getting a high interest rate, creating a partial counter-pressure). The main reason to target a fixed interest rate is to minimize selfish-validating risks, as there would be no way for a validator to benefit themselves simply by hurting the interests of other validators. A hybrid route in proof of stake could combine these guarantees, for example providing selfish mining protection if possible but sticking to a hard minimum target of 5% stake participation.
Now, we can also get to discussing the difference between redistributing and burning transaction fees. It is clear that, in expectation, the two are equivalent: redistributing 50 ETH per day and inflating 50 ETH per day is the same as burning 50 ETH per day and inflating 100 ETH per day. The tradeoff, once again, comes in the variance. If fees are redistributed, then we have more certainty about the supply, but less certainty about the level of security, as we have certainty about the size of the validation incentive. If fees are burned, we lose certainty about the supply, but gain certainty about the size of the validation incentive and hence the level of security. Burning fees also has the benefit that it minimizes cartel risks, as validators cannot gain as much by artificially pushing transaction fees up (eg. through censorship, or via capacity-restriction soft forks). Once again, a hybrid route is possible and may well be optimal, though at present it seems like an approach targeted more toward burning fees, and thereby accepting an uncertain cryptocurrency supply that may well see low decreases on net during high-usage times and low increases on net during low-usage times, is best. If usage is high enough, this may even lead to low deflation on average.

Leave a Reply